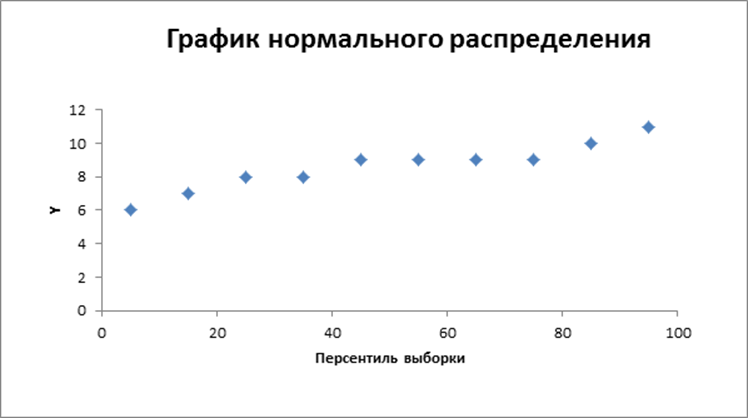
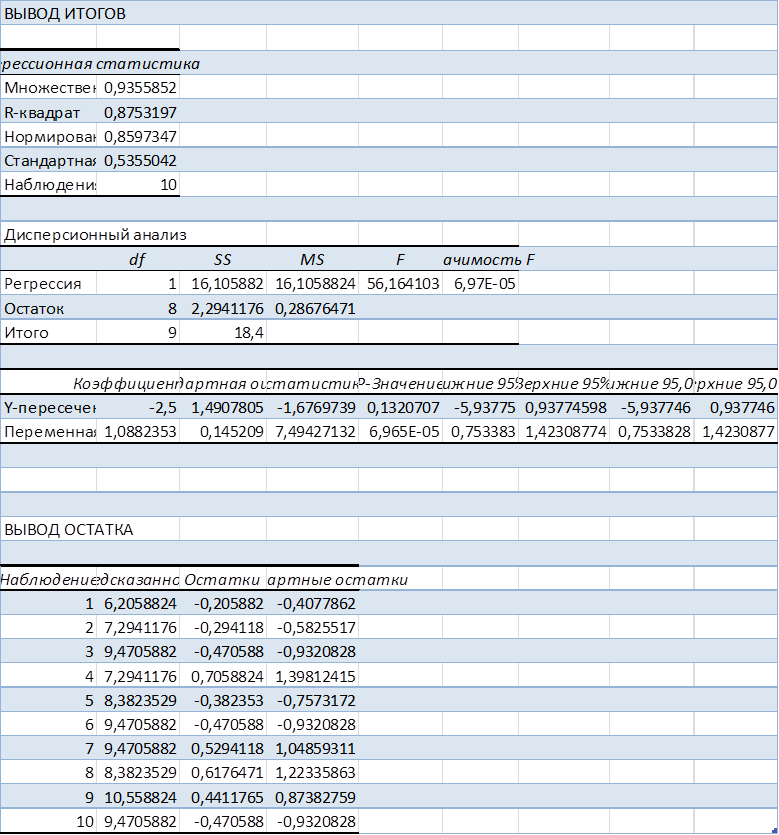
Влияние факторов производства на объем выпуска

Вариант 4. Влияние факторов производства на совокупный объем выпуска товара.

Для определения зависимости между закупом сахара в месяц ( переменная x, измеряется в тысячах), и выпуском кондитерских изделий (переменная y, измеряется в тоннах) были проведены исследования за 10 месяцев.

Построение уравнения регрессии содержит два этапа:

·  Определение вида регрессии f(x)

·  Вычисление коэффициентов уравнения регрессии, являющихся оценками для коэффициентов функции регрессии.

Построение уравнения регрессии подразумевает наличие между переменными Х и У статистической зависимости. Коэффициент корреляции (r ) характеризует тесноту линейной зависимости. Вычислим, используя функцию в Excel — КОРРЕЛ.

1)  Оценку параметров модели парной регрессии вычислим уравнением линейной регрессии:

= f(x) = b0+b1*x

В Excel это функция ЛИНЕЙН

2)  Функции Excel для вычисления коэффициентов парной линейной регрессии:

·  коэффициент b0 вычислим с помощью функции ОТРЕЗОК

·  коэффициент b1 (эластичность) вычислим с помощью функции НАКЛОН

·  стандартные ошибки коэффициентов регрессии S с помощью функции

СТОШYX

Оценка качества построенной модели имеет несколько этапов

А) анализ адекватности модели в целом

Б) анализ точности определения оценок коэффициентов

В) проверка статистической значимости коэффициентов регрессии

Г) определение доверительных интервалов для зависимой переменной

I. Изменение результативного признака y обусловлено вариацией факторного признака x. Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака характеризует коэффициент детерминации R2. Для линейной зависимости коэффициент детерминации равен квадрату коэффициента корреляции:

R2 = rxy2, где rxy — коэффициент корреляции.

R2 = 0.942 =0.875 , означает, что 87.5% случаев изменения х приводит к изменению у. Другими словами, точность подбора уравнения регрессии – высокая.

II. Анализ точности определения оценок коэффициентов регрессии.

Для вычислений средних значений используется функция Excel СРЕЗНАЧ (диапазон ячеек)

Отсюда найдем:

Sb0 – стандартное отклонение случайной величины b0

Sb0 = S 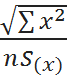= 0.54 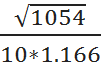= 1.49

Sb1 – стандартное отклонение случайной величины b1

Sb1 = 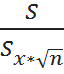= =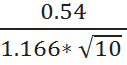0.15

III. а)Значимость коэффициентов проверяют по расчетам критерия Фишера, и сравнением его с табличным значением:

F=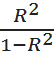*(n-2) = 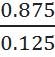*8 = 56
Fкрит= FРАСПРОБ(α, k, n-k-1) α= 0,05

степень свободы k1 = 1 и k2 = 8

С помощью функции FРАСПРОБ вычислим F0.95; 1; 8 = 5,32

Fрасчет ≥ Fтабл 56 ≥ 5,32

Неравенство выполняется и поэтому уравнение регрессии значимо.

б) так же используют t – критерий Стьюдента, найденный по данным наблюдениям и сравнением его с табличным значением.

Табличное значение определяется в зависимости от уровня значимости (α) и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n-число наблюдений.
tкрит (n-m-1;α/2) = (8;0.025) = 2.306

tb1= = = 7.49

Поскольку 7.49 > 2.306, то статистическая значимость коэффициента регрессии b1 подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

tb0 = = =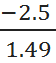1.68

Поскольку 1.68 < 2.306, то статистическая значимость коэффициента регрессии b0 — не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента). Это означает, что в данном случае коэффициентом b0 можно пренебречь.

IV. определение доверительных интервалов для зависимой переменной

Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(1.09 — 2.306 • 0.15; 1.09 + 2.306 • 0.15)
(0.753;1.423)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — tкрит Sa; a + tкрит Sa)
(-2.5 — 2.306 • 1.49; -2.5 + 2.306 • 1.49)
(-5.938;0.938)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

Постоим графическое изображение построенной модели.