Теория игр задачи

№1

1.Ученый совет институт состоит из членов. Сколько может образоваться коалиций из членов.

Варианты заданий (n, m): (11,4):(12,4);(12,5);(11,5);(11,6);(13,3),(13,4);(13,5);14,4);(14,5)/

4 акционера имеют (a, b,c, d) акций. Найти вектор Шепли в борьбе за формирование контрольного пакета.

Варианты заданий (a, b,c, d):

(10,20,30,40);(15,25,35,45);(30.30,30,10);(30,20,20,30);(10,10,40,40);(20,20,20,40);(10,10,10,70);(15,15,15,55);(25,25,25,25):(30,30,20,30).

3.Составить таблицу наподобие в дис. Курно на стр.27 (предварительно рассказав о этой таблице), составить варианты заданий-может сами студенты и составят?

№2

1).Проанализировать биматричную игру 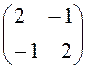: найти чистые стратегии, доминирующие одна другую; найти множество Парето чистых стратегий, равновесие Нэша, графически множество Парето, переговорное множество, максиминные стратегии и максиминные выигрыши игроков.

2).Для дуополии Курно, как для биматричной игры найти: множество Парето, стратегии Курно, Штакельберга, равновесие Нэша;

3).Для модели Курно как для — персонной игры найти то же, что в задаче 2.

№ 3.

1).Найти решение матричной игры 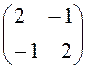с нулевой суммой: аналитически, графически, исследовать игру на риск, написать двойственную пару соответствующих задач ЛП;

2)Пусть в игре НИМ Первый своим первым ходом берет 2 спичку из группы в 2 спички. Опишите перехват 2 –м игроком инициативы в игре и доведение игры до его победы.