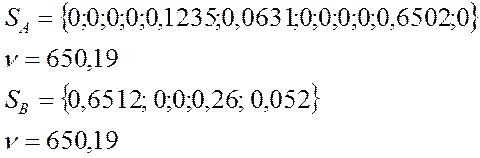Задачи по экономике | Теория игр лабораторная

Задача.

Предприятие может выпускать несколько видов продукции: A1, A2, A3, …, получая при этом прибыль. Величина прибыли определяется состоянием спроса («природой» рынка), который может находиться водном изнескольких возможных состояний: B1, B2, B3, …

Зависимость величины прибыли от вида выпускаемой продукции и состояния рынка представлена в платежных матрицах.

Рассмотрите таблицу как матричную игру «предприятие (игрок А) против «природы» рынка (игрок В)». Для заданной платежной матрицы:

1) найдите нижнюю и верхнюю цены игры;

2) определите оптимальные смешанные стратегии игроков с помощью сведéния игры к задаче линейного программирования;

3) интерпретируйте полученные результаты применительно к рассматриваемой экономической задаче.

	В1	В2	В3	В4	В5
А1	313	275	180	373	424
А2	515	321	335	282	520
А3	338	284	750	229	710
А4	560	300	730	694	500
А5	679	311	732	647	290
А6	750	465	594	403	576
А7	384	486	383	436	286
А8	296	737	325	635	650
А9	552	636	636	540	639
А10	561	288	792	636	299
А11	638	810	708	670	712
А12	506	445	567	504	510

Решение:

	В1	В2	В3	В4	В5	min
А1	313	275	180	373	424	180
А2	515	321	335	282	520	282
А3	338	284	750	229	710	229
А4	560	300	730	694	500	300
А5	679	311	732	647	290	290
А6	750	465	594	403	576	403
А7	384	486	383	436	286	286
А8	296	737	325	635	650	296
А9	552	636	636	540	639	540
А10	561	288	792	636	299	288
А11	638	810	708	670	712	638
А12	506	445	567	504	510	445
max	750	737	792	694	712

Исходная платежная матрица.

Т. к =638, а =694, игра не имеет седловой точки, нижняя цена игры – 638, верхняя – 695.

В данной игре нет дублирующих и доминируемых стратегий.

Решаеи игру путем решения пары двойственных задач линейного программирования.

Сформулируем прямую задачу линейного программирования:

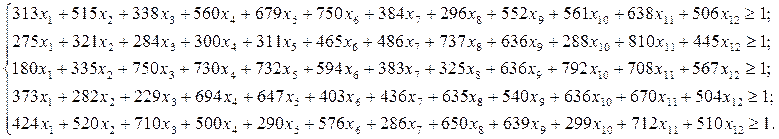
xi0, .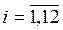

Коэффициенты системы уравнений образуют транспонированную матрицу исходной платежной матрицы:

313

515

338

560

679

750

384

296

552

561

638

506

275

321

284

300

311

465

486

737

636

288

810

445

180

335

750

730

732

594

383

325

636

792

708

567

373

282

229

694

647

403

436

635

540

636

670

504

424

520

710

500

290

576

286

650

639

299

712

510

На рабочем листе Excel запишем исходную и транспонированную платежную матрицу.

Исходная платежная матрица.

В1

В2

В3

В4

В5

А1

313

275

180

373

424

А2

515

321

335

282

520

А3

338

284

750

229

710

А4

560

300

730

694

500

А5

679

311

732

647

290

А6

750

465

594

403

576

А7

384

486

383

436

286

А8

296

737

325

635

650

А9

552

636

636

540

639

А10

561

288

792

636

299

А11

638

810

708

670

712

А12

506

445

567

504

510

Транспонированная платежная матрица

313

515

338

560

679

750

384

296

552

561

638

506

275

321

284

300

311

465

486

737

636

288

810

445

180

335

750

730

732

594

383

325

636

792

708

567

373

282

229

694

647

403

436

635

540

636

670

504

424

520

710

500

290

576

286

650

639

299

712

510

В ячейках A22:L26 будут храниться значения X1, X2, X3, Х4, Х5, Х6, Х7, Х8, Х9, Х10, Х11, Х12. Пока запишем в эти ячейки нулевые значения.

В ячейку О23 введем формулу =A23+B23+C23+D23+E23+F23+G23+H23+H23+I23+J23+K23+L23. То есть в этой ячейке будет храниться значение целевой функции.

Вычислим левые части неравенств системы. Для этого все элементы каждой строки транспонированной платежной матрицы нужно умножить на значения X1, X2, X3, Х4, Х5, Х6, Х7, Х8, Х9, Х10, Х11, Х12.

В Excel это можно сделать при помощи встроенной функции СУММПРОИЗВ().

В ячейке M15 вычислим левую часть первого ограничения из системы.

Аналогично вычислим левые части оставшихся ограничений в ячейках M16, M17, M18, M19.

Решением задачи линейного программирования будут такие значения X1, X2, X3, Х4, Х5, Х6, Х7, Х8, Х9, Х10, Х11, Х12, при которых целевая функция принимает минимальное значение, и выполняются все неравенства системы. Поиск оптимального решения задачи линейного программирования в Excel найдем при помощи надстройки «Поиск решения».

313

515

338

560

679

750

384

296

552

561

638

506

1

1

275

321

284

300

311

465

486

737

636

288

810

445

1,1155

1

180

335

750

730

732

594

383

325

636

792

708

567

1,0824

1

373

282

229

694

647

403

436

635

540

636

670

504

1

1

424

520

710

500

290

576

286

650

639

299

712

510

1

1

Целевая функция = 0,0015379

Из решения задачи линейного программирования находим цену игры и оптимальную стратегию Sa по формулам:

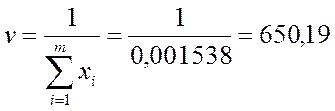
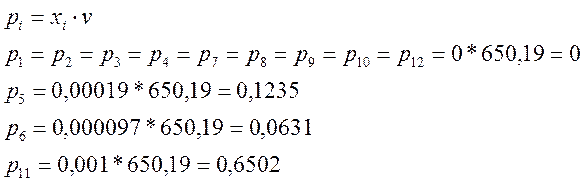
Аналогично находим оптимальную стратегию SВ игрока В:

Учитывая, что игрок В стремится минимизировать свой проигрыш, получаем задачу линейного программирования:

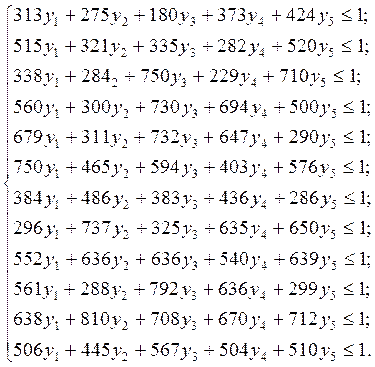
yj0, .

На рабочем листе Excel запишем исходную платежную матриц

В1

В2

В3

В4

В5

А1

313

275

180

373

424

А2

515

321

335

282

520

А3

338

284

750

229

710

А4

560

300

730

694

500

А5

679

311

732

647

290

А6

750

465

594

403

576

А7

384

486

383

436

286

А8

296

737

325

635

650

А9

552

636

636

540

639

А10

561

288

792

636

299

А11

638

810

708

670

712

А12

506

445

567

504

510

Y1

Y2

Y3

Y4

Y5

0

0

0

0

0

В ячейках A37:E37 будут храниться значения Y1, Y2, Y3, Y4, Y5. Пока запишем в эти ячейки нулевые значения.

В ячейке O38 введем формулу =A38+B38+C38+D38+E38. То есть в этой ячейке будет храниться значение целевой функции.

Вычислим левые части неравенств системы. Для этого все элементы каждой строки платежной матрицы нужно умножить на значения Y1, Y2, Y3, Y4, Y5.

В ячейке G17 вычислим левую часть первого ограничения из системы.

Аналогично вычислим левые части оставшихся ограничений в ячейках G18, G19, G20, G21, G22, G23, G24, G25, G26 ,G27,G28

В1

В2

В3

В4

В5

А1

313

275

180

373

424

0,5144

1

А2

515

321

335

282

520

0,6988

1

А3

338

284

750

229

710

0,506

1

А4

560

300

730

694

500

0,9102

1

А5

679

311

732

647

290

1

1

А6

750

465

594

403

576

1

1

А7

384

486

383

436

286

0,6035

1

А8

296

737

325

635

650

0,6199

1

А9

552

636

636

540

639

0,8511

1

А10

561

288

792

636

299

0,8718

1

А11

638

810

708

670

712

1

1

А12

506

445

567

504

510

0,7777

1

Решением задачи линейного программирования будут такие значения Y1, Y2, Y3, Y4, Y5, при которых целевая функция принимает максимальное значение, и выполняются все неравенства системы. Поиск оптимального решения задачи линейного программирования в Excel найдем при помощи надстройки «Поиск решения».

Y1

Y2

Y3

Y4

Y5

0,001056

0

0

0

0

Из решения задачи линейного программирования находим цену игры и оптимальную стратегию Sв по формулам:

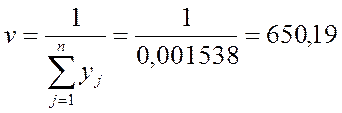
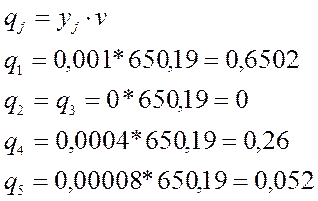
Ответ:

Теория игр лабораторная

Наташа

Узнать стоимость за 15 минут

Распродажа дипломных

Подпишись на наш паблик в ВК

Нужна работа?

313	515	338	560	679	750	384	296	552	561	638	506
275	321	284	300	311	465	486	737	636	288	810	445
180	335	750	730	732	594	383	325	636	792	708	567
373	282	229	694	647	403	436	635	540	636	670	504
424	520	710	500	290	576	286	650	639	299	712	510

313	515	338	560	679	750	384	296	552	561	638	506
275	321	284	300	311	465	486	737	636	288	810	445
180	335	750	730	732	594	383	325	636	792	708	567
373	282	229	694	647	403	436	635	540	636	670	504
424	520	710	500	290	576	286	650	639	299	712	510

313	515	338	560	679	750	384	296	552	561	638	506	1	1
275	321	284	300	311	465	486	737	636	288	810	445	1,1155	1
180	335	750	730	732	594	383	325	636	792	708	567	1,0824	1
373	282	229	694	647	403	436	635	540	636	670	504	1	1
424	520	710	500	290	576	286	650	639	299	712	510	1	1

	В1	В2	В3	В4	В5
А1	313	275	180	373	424	0,5144	1
А2	515	321	335	282	520	0,6988	1
А3	338	284	750	229	710	0,506	1
А4	560	300	730	694	500	0,9102	1
А5	679	311	732	647	290	1	1
А6	750	465	594	403	576	1	1
А7	384	486	383	436	286	0,6035	1
А8	296	737	325	635	650	0,6199	1
А9	552	636	636	540	639	0,8511	1
А10	561	288	792	636	299	0,8718	1
А11	638	810	708	670	712	1	1
А12	506	445	567	504	510	0,7777	1

313	515	338	560	679	750	384	296	552	561	638	506
275	321	284	300	311	465	486	737	636	288	810	445
180	335	750	730	732	594	383	325	636	792	708	567
373	282	229	694	647	403	436	635	540	636	670	504
424	520	710	500	290	576	286	650	639	299	712	510

313	515	338	560	679	750	384	296	552	561	638	506
275	321	284	300	311	465	486	737	636	288	810	445
180	335	750	730	732	594	383	325	636	792	708	567
373	282	229	694	647	403	436	635	540	636	670	504
424	520	710	500	290	576	286	650	639	299	712	510

313	515	338	560	679	750	384	296	552	561	638	506
275	321	284	300	311	465	486	737	636	288	810	445
180	335	750	730	732	594	383	325	636	792	708	567
373	282	229	694	647	403	436	635	540	636	670	504
424	520	710	500	290	576	286	650	639	299	712	510

313	515	338	560	679	750	384	296	552	561	638	506
275	321	284	300	311	465	486	737	636	288	810	445
180	335	750	730	732	594	383	325	636	792	708	567
373	282	229	694	647	403	436	635	540	636	670	504
424	520	710	500	290	576	286	650	639	299	712	510