Теорема гаусса-маркова и метод максимального правдоподобия

3.  Условие гомоскедастичности (равноизменчивости) возмущения или, что то же самое, переменной yi:

4. Возмущения ei и ej (или переменные у i и у j) некоррелированы:

5. Возмущение ei (или переменная уi) есть НРСВ.

Модель, для которой выполняются все пять предпосылок, называется нормальной классической линейной регрессионной моделью (НКЛРМ). Для получения уравнения регрессии достаточно предпосылок 1-4. Предпосылка 5 необходима для оценки точности уравнения и его параметров.

2.4. Качество оценок параметров bo, b1 и s2: теорема Гаусса-Маркова и метод максимального правдоподобия

Оценкой модели (2.15) по выборке является уравнение регрессии (2.2): = bo +b1x. Оценки bo и b1 параметров bo и b1 находятся по МНК (см. выше).

Качество уравнения (2.2) оценивается по нескольким показателям. Один из них — s2 — выборочная несмещенная оценка остаточной дисперсии (дисперсии возмущений) s2:

где — групповая средняя, найденная с помощью уравнения регрессии; ei = (-yi) — выборочная оценка возмущения (остаток регрессии).

Заметим, что в уравнении (2.19) число степеней свободы k=n-m=n-2, т. к. две степени теряются (связываются) при определении двух параметров: bo и b1.

Вопрос: являются ли оценки bo, b1 и s2 параметров bo, b1 и s2 наилучшими? Ответ на этот вопрос дает теорема Гаусса-Маркова и привлечение метода максимального правдоподобия (табл. 2.3).

Теорема Гаусса-Маркова. Если регрессионная модель (2.15) удовлетворяет предпосылкам 1-4, то оценки уравнения (2.7) bo, b1 имеют наименьшую дисперсию в классе всех линейных несмещенных оценок, т. е. являются эффективными.

Таблица 2.3

Показатели качества оценок bo, b1, s2

Кратко охарактеризуем метод максимального правдоподобия (ММП). Для его применения допустим выполнение предпосылки 5: значения уi — независимые СВ с НЗР, математическим ожиданием М(уi) = bo+b1хi и постоянной дисперсией возмущений s2.. В основе метода лежит функция правдоподобия:

L(y1, x1, … , yn, xn, bo, b1, s2) =

=

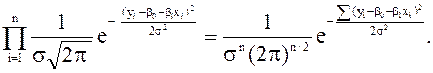
В качестве оценок параметров bo, b1, s2 в ММП принимаются такие значения, , , , которые максимизируют функцию правдоподобия L. Для нашей функции L максимум достигается при условии минимума ее показателя степени: å (yi — bo — b1xi)2 ® min, что совпадает с условием МНК для определения bo и b1

Оценка по ММП также находится из условия минимума L. Для ее нахождения используем уравнение ¶L/¶s = 0, откуда имеем:

2.5. Доверительный интервал для функции регрессии

Доверительный интервал для функции регрессии, т. е. для условного МО Мх(Y), с заданной доверительной вероятностью (надежностью) g=1-a должен покрыть неизвестное значение Мх(Y).

Представим уравнение регрессии в отклонениях в виде:

Дисперсия суммы независимых СВ равна сумме дисперсий этих СВ. Учитывая этот факт, а также то, что (х — ) — неслучайная величина, найдем выражение для дисперсии :

Найдем выражения для двух дисперсий правой части уравнения (2.22). Дисперсия выборочной средней :

Дисперсия коэффициента регрессии :

Суммируя уравнения (2.23) и (2.24), получаем искомую дисперсию (s2 заменена ее оценкой s2):

Обратим внимание на то, что дисперсия (x) является функцией от переменной х, и зависимость эта квадратичная. Минимума дисперсия (x) достигает при х = , а по мере удаления х от своего среднего значения (и в меньшую, и в большую сторону) дисперсия возрастает пропорционально квадрату х (рис. 2.2).

Допуская предпосылки 1-5 регрессионного анализа, получаем статистику t = (— Мх(Y)) /, которая имеет t-распределение Стьюдента с k=n-2 степенями свободы. Теперь можно построить доверительный интервал для условного МО Мх(Y):
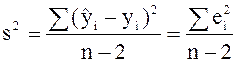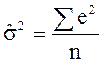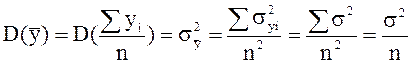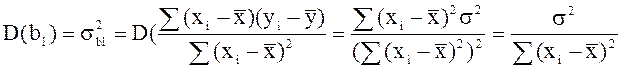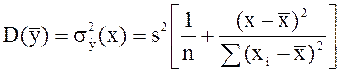