Парный регрессионный анализ
Вопросы для самоконтроля
1. Дайте определения модели, математической модели, моделирования, эконометрической модели.
2. Охарактеризуйте идею моделирования по принципу черного ящика, его связь с эконометрической моделью, типы переменных.
3. Раскройте содержание понятия: регрессионная модель.
4. Чем обусловлены проблемы получения больших однородных выборок?
5. Что такое пространственные и временные данные?
6. В чем суть гомоскедастичности дисперсии ошибок?
7. Каким четырем условиям удовлетворяют (или нет) ошибки регрессии?
8. Какие методы (приемы) сочетаются в процедуре спецификации функции, сколько их?
9. Назовите достоинства и недостатки линейных регрессионных моделей.
10. Какие линейные регрессионные модели называются классическими?
11. В чем отличие системы одновременных уравнений регрессии от простого набора регрессионных уравнений?
12. Что такое лаговая переменная, чем она отличается от обычной объясняющей переменной?
13. В чем суть процедуры спецификации модели?
14. В чем суть процедуры верификации модели, назовите несколько приемов верификации.
![]() 2. Парный регрессионный анализ
2. Парный регрессионный анализ
2.1. Линейная парная регрессия
Методы и модели регрессионного анализа занимают центральное место в математическом инструментарии эконометрики. Наиболее часто используется парная регрессия, когда рассматривается пара переменных: одна объясняющая (синонимы — входная, экзогенная, регрессор) переменная Х и одна – объясняемая (синонимы — выходная, результирующая) переменная Y – обязательно случайная величина.
Регрессией называют функцию, отражающую зависимость математического ожидания (МО) СВ Y от значений Х (такую зависимость называют также корреляционной). По определению регрессия есть условное МО СВ Y:
|
Мх(Y) = j(х). |
(2.1) |
На практике точно не известно условное МО СВ Y, т. е. функция j(х). Поэтому можно говорить лишь о приближенном построении — оценке такой функции. Исходными данными для этого служат n пар значений Х и Y: xi и yi при i=1, 2, … , n.
В случае парной линейной регрессии в качестве оценки — выборочного уравнения регрессии — принимается прямая линия:
|
|
(2.2) |
Неизвестные параметры bo и b1, как правило, определяются методом наименьших квадратов: значения параметров должны доставлять минимум сумме квадратов отклонений наблюденных значений yi от теоретических значений ![]() , определяемых регрессией (2.2):
, определяемых регрессией (2.2):
|
S(bo, b1) = å ( |
(2.3) |
Теоретически для оценки параметров bo и b1 можно использовать и метод наименьших модулей отклонений å ç![]() — yiç. Однако метод наименьших квадратов (МНК), во-первых, проще, во-вторых, его применение обосновывается законом больших чисел, в-третьих, позволяет проводить глубокий анализ качества эконометрической модели.
— yiç. Однако метод наименьших квадратов (МНК), во-первых, проще, во-вторых, его применение обосновывается законом больших чисел, в-третьих, позволяет проводить глубокий анализ качества эконометрической модели.
Для отыскания значений параметров bo и b1 эконометрической модели (2.2) с помощью МНК приравниваем нулю частные производные S по bo и b1 и получаем систему двух уравнений:
|
¶S/¶ bo = 2å (bo +b1xi — yi) = 0 ¶S/¶ b1 = 2å (bo +b1xi — yi) xi = 0. |
(2.4) |
Отсюда после преобразований получаем систему двух линейных уравнений с двумя неизвестными bo и b1:
|
bon + b1åxi = å yi, boåxi + b1å |
(2.5) |
Разделим 1-е уравнение на n и получим полезное соотношение: линия регрессии проходит через точку средних значений (![]() ,
, ![]() ):
):
|
|
(2.6) |
Разрешая (2.6) относительно bo, подставляя это значение во 2-е уравнение системы (2.5), получим искомые формулы для расчета значений параметров уравнения регрессии:
|
bo = b1 = |
(2.7) |
где sx2 — выборочная дисперсия переменной Х:
|
|
(2.8) |
![]() — выборочная ковариация:
— выборочная ковариация:
|
|
(2.9) |
Параметр b1 называется коэффициентом регрессии (выборочным). Он показывает, на сколько единиц в среднем возрастет (уменьшится) ![]() при увеличении х на одну единицу.
при увеличении х на одну единицу.
Параметр b0 в зависимости от задачи может иметь смысл, а может и не иметь. Например, если ![]() — расход электроэнергии, а х – объем производства, то параметр b0 — условно-постоянный расход электроэнергии при нулевом производстве. Если b0<0, то экономического смысла он, как правило, не имеет.
— расход электроэнергии, а х – объем производства, то параметр b0 — условно-постоянный расход электроэнергии при нулевом производстве. Если b0<0, то экономического смысла он, как правило, не имеет.
Пример 2.1 [4, с.10]. Построить уравнение парной линейной регрессии для данных табл. 2.1, где Y — расходы на покупку продовольственных товаров, % от общих расходов и Х — среднедневная зарплата, руб./чел.×сут.
Таблица 2.1
Условные данные по субъектам России за 199Хг.
|
Субъект РФ |
Y |
X |
|
Субъект-1 |
68,8 |
45,1 |
|
Субъект-2 |
61,2 |
59,0 |
|
Субъект-3 |
59,9 |
57,2 |
|
Субъект-4 |
56,7 |
61,8 |
|
Субъект-5 |
55,0 |
58,8 |
|
Субъект-6 |
54,3 |
47,2 |
|
Субъект-7 |
49,3 |
55,2 |
Расчеты удобно проводить с использованием таблицы типа табл. 2.2.
Таблица 2.2
Промежуточные расчетные данные
|
№ п/п |
уi |
xi |
уi xi |
|
|
|
yi — |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
68,8 |
45,1 |
3102,88 |
2034,01 |
4733,44 |
61,3 |
7,5 |
|
2 |
61,2 |
59,0 |
3610,80 |
3481,00 |
3745,44 |
56,5 |
4,7 |
|
3 |
59,9 |
57,2 |
3426,28 |
3271,84 |
3588,01 |
57,1 |
2,8 |
|
4 |
56,7 |
61,8 |
3504,06 |
3819,24 |
3214,89 |
55,5 |
1,2 |
|
5 |
55,0 |
58,8 |
3234,00 |
3457,44 |
3025,00 |
56,5 |
-1,5 |
|
6 |
54,3 |
47,2 |
2562,96 |
2227,84 |
2948,49 |
60,5 |
-6,2 |
|
7 |
49,3 |
55,2 |
2721,36 |
3047,04 |
2430,49 |
57,8 |
-8,5 |
|
Итого |
405,2 |
384,3 |
22162,34 |
21338,41 |
23685,76 |
405,2 |
0,0 |
|
Средн. |
57,89 |
54,90 |
3166,05 |
3048,34 |
3383,68 |
— |
— |
|
s |
5,74 |
5,86 |
Решение. В табл. 2.2 графы 2 и 3 — наблюденные пары значений переменных Y и Х, графы 4-6 вычисляются непосредственно на основе граф 2 и 3. Остальные графы в этом примере не используются.
По формулам (2.7) рассчитаем параметры регрессии b0 и b1, получим искомое уравнение регрессии:
|
|
(2.10) |
Смысл параметра уравнения b1: при увеличении среднесуточного дохода на 1 руб. расход на продовольствие сократится на 0,35% от общей суммы среднесуточного расхода. Свободный член b0 смысла не имеет.
2.2. Связь коэффициентов регрессии и корреляции
Если значение bo из формул (2.7) подставить в уравнение регрессии (2.2), то после преобразований получим уравнение регрессии в отклонениях (прямая проходит через начало координат — точку ( ![]() )).
)).
Преобразуем это уравнение: разделим обе части на sy, умножим и разделим правую часть на sx, получим:
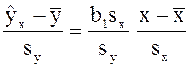 .
.
|
где коэффициент r = b1 sx/sy показывает, на сколько величин sy изменится в среднем Y, если Х увеличится на одно значение sx. |
(2.11) |
Другой вариант формулы для расчета r:
|
|
(2.12) |
Статистика r — выборочный коэффициент корреляции — отражает тесноту статистической связи случайных величин Х и Y. Свойства коэффициента корреляции (рис. 2.1):
1. -1 £ r £ 1. Чем ближе модуль ç r ç к 1, тем теснее связь Х и Y.
2. Если r = ± 1, то связь между Х и Y — функциональная и линейная.
3. Если r = 0, то линейная корреляционная связь между СВ Х и Y отсутствует.
4. Коэффициент r является непосредственной оценкой генерального коэффициента корреляции r между Х и Y лишь в случае двухмерного НЗР случайной величины (Х, У). В других случаях r не является строгой мерой взаимосвязи переменных.
у у у




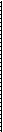


 r = +1 r » +0,8 r » +0,5
r = +1 r » +0,8 r » +0,5
 |


 х х х
х х х
а) б) в)



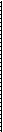
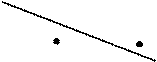
 у r = -1 у r » -0,8 у r » -0,5
у r = -1 у r » -0,8 у r » -0,5
 |
 |
 |


 х х х
х х х
г) д) е)
Рис. 2.1. Примеры полей корреляции и значений r
Пример 2.2. По данным табл. 2.1 и примера 2.1 рассчитать значение коэффициента корреляции r. Для расчета используем формулу (2.11): r = b1 sx / sy. Неизвестные СКО sx и sy рассчитаем по формулам и данным табл. 2.1:
![]() .
.
![]() .
.
Окончательно: r = b1 sx / sy = -0,35×5.86 / 5,74 = -0,36.
Данное значение r характеризует связь между Х и Y как умеренную и обратную (см. рис. 2.1.е).
2.3. Основные положения регрессионного анализа
Напомним, что парная регрессионная модель представляется в виде:
|
Y = j(Х) + e, |
(2.13) |
где e — СВ — возмущение, ошибка, характеризующая отклонение СВ Y от функции регрессии j(Х) — условного математического ожидания Мх(Y). В линейном регрессионном анализе j(Х) линейна относительно оцениваемых параметров:
|
Мх(У) = j(Х) = b0 +b1х. |
(2.14) |
Пусть для оценки параметров регрессии взята выборка из n пар (xi, yi). Тогда линейная парная регрессионная модель имеет вид:
|
yi = b0 +b1хi + ei. |
(2.15) |
Теперь рассмотрим основные предпосылки регрессионного анализа:
1. В модели (2.15) возмущение ei, а значит и зависимая переменная yi, есть величина случайная, а объясняющая переменная хi — величина неслучайная, но принимающая различные значения.
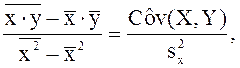
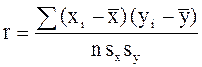 .
.

