Доклад по эконометрике
ВВЕДЕНИЕ
Логарифмирование (вычисление логарифма) применимо в различных областях человеческой деятельности: астрономия, научные и инженерных расчеты, решение дифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация (замена объектов близкими к сходным) различных зависимостей, теория вероятностей и т. д. Широко используется в эконометрике — науке, изучающей количественные и качественные экономические взаимосвязи между явлениями и процессами.
Актуальность логарифмирования объясняется уникальными свойствами логарифмов, которые определили их широкое использование для существенного упрощения трудоёмких вычислений[3]. При переходе «в мир логарифмов» умножение заменяется на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня преобразуются соответственно в умножение и деление на показатель степени.
Целью работы является описание применения логарифмов в экономико-статистических моделях.
Для достижения цели требуется решение следующих задач:
— дать определение понятию логарифмов;
— описать свойства логарифмов;
— обосновать целесообразность логарифмирования;
— привести пример логарифмирования при анализе производственных функций.
1.Понятие и свойства логарифма
Логари́фм числа b по основанию a определяется как показатель степени, в которую надо возвести основание a, чтобы получить число b . Обозначение: logab . Логарифмическая функция logax обратна показательной функции y = ax (a>0, a≠1), при a>1 функция возрастает. Графики взаимообратных функций симметричны относительно прямой y=x (рис.1).
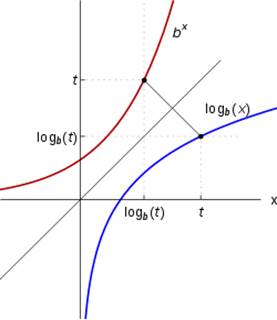
Рис.1 Логарифмическая функция обратна к показательной [1]
Логарифмировать имеем право только положительные числа или выражения. Примеры:
log42=1/2; log2(1/2)= -1; log3(1/81) = -4, так как 3-4 = (1/3)4= 1/81
Логарифмы 0 и отрицательных чисел не определены. Примеры:
log 20 = нет, log 5 (-2)= нет (0 или отрицательное число не можем получить при возведении в степень).
Свойства логарифмов:
1) loga1=0. Пример: log31=0
2) logaa=1. Пример: log33=0
3) Логарифм произведения равен сумме логарифмов множителей:
loga(x*y)= logax + logay
Пример: log2(4*2) = log24 + log2 2 = 2+1 = 3
4) Логарифм частного (дроби) равен разности логарифмов числителя и знаменателя:
loga(x/y) = logax — logay
Пример: log4(32/2) = log432 — log42 = log4(64/2) — log42 = log464 — log42 — log42 = 3 – 2*(1/2) = 2
5) Если логарифмируем степень, то показатель степени можно вынести за знак логарифма в качестве множителя:
logaxp=p*logax
Пример: log1642 = 2 log164 = 2*(1/2) = 1
6) Из определения логарифма следует основное логарифмическое тождество:
a logax=x
Прологорифмируем левую часть этого равенства по основанию b:
logb(alogax) = logbx
logax * logb a = logbx
Формула перехода к другому основанию:
logax = logbx/logb a
Пример:
7) Если основание логарифма 10 , то такой логарифм называется десятичным
log10x= lg x
Если основание логарифма – число Эйлера e=2,7.., то это натуральный логарифм:
logex=ln x
2. Логарифмы в эконометрике
Если переменная представляет некоторое положительное количество, то ее в большинстве случаев логарифмируют. Примеры: цены, объем производства, масса, зарплата, валютный курс и т. д. и т. п. (Но не годятся: процентные ставки, сальдо экспорта/импорта, темп роста ВВП, температура воздуха…). Причины:
1) Удобство аддитивного представления*. Например, было M/P = kY. Стало:
ln(M) — ln(P) = ln(k) + ln(Y),
то есть модель стала линейной (в новых переменных — логарифмах)
2) Без логарифмирования динамика переменной имеет экспоненциальный тренд, а в логарифмах – линейный. Например, рождаемость — относительный показатель по отношению к имеющемуся населению — в среднем довольно стабильна, поэтому рост населения близок к экспоненциальному. Логарифмируя получим примерно линейный тренд. Первые разности такого ряда — это логарифмический темп прироста
3) Без логарифмирования ошибки гетероскедастичны (наблюдение неоднородно, дисперсия (мера разброса) случайной ошибки регрессионной модели непостоянно), что приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов **. Следовательно статистические выводы о качестве полученных оценок могут быть неадекватными. В логарифмах дисперсия постоянна, то есть отсутвует рост дисперсии ошибки с увеличением значения независимой переменной.
4) Логарифмические темпы прироста ln(X[t]) — ln(X[t-1]) похожи на обычные (X[t] — X[t-1])/X[t-1], но имеют ряд преимуществ. Так, для финансовых рядов их распределение гораздо больше похоже на нормальное***.
5) Если и зависимая (эндогенная) переменная y и объясняющая (экзогенная) переменная х в регрессионной модели у = αxβ **** в логарифмах, то коэффициент при объясняющей переменной не что иное как эластичность.[1] Стандартным и широко используемым подходом к анализу функций данного рода в эконометрике является логарифмирование по экспоненте (по основанию е = 2,71828: ln y = ln α + b1*ln x, заменив In a = bо и добавив в модель случайную погрешность ε получим так называемую двойную логарифмическую модель:
ln y = b0 + b1lnх + ε
Коэффициент b1 является константой, указывая на постоянную эластичность*****. Суть полученных выводов наглядно представлена на рис.2
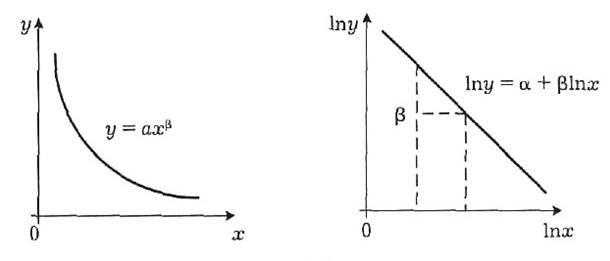
Рис.2 Регрессионная модель и двойная логарифмическая модель
Данная модель легко обобщается на большее число переменных:
ln y = b0 + b1lnх + b2lnх + ε
Коэффициенты bо и b1 являются эластичностями переменной y по переменным x1 и х2, соответственно. Нередко данная модель используется при анализе производственных функций. Например, хорошо известна производственная функция Кобба-Дугласа ******:
In V = In A + αln К + βln L
Здесь α и β – коэффициенты эластичности выпуска продукции по затратам капитала и труда соответственно. Сумма этих коэффициентов является таким важным экономическим показателем, как отдача от масштаба. При α + β = 1 говорят о постоянной отдаче от масштаба (во сколько раз увеличиваются затраты ресурсов, во столько же раз увеличивается выпуск). При α + β < 1 имеет место убывающая отдача от масштаба (увеличение объема выпуска меньше увеличения затрат ресурсов). При α + β > 1 – возрастающая отдача от масштаба (увеличение объема выпуска больше увеличения затрат ресурсов). [2]
*[Аддитивная модель – это модель, в которую факторы входят в виде алгебраической суммы.
Примером такого типа модели может стать модель товарного баланса: Vреал=Р нач+Vпр-Р кон, где
Vреал — объем реализации (за период),
Рнач — остатки нереализованной продукции на начало периода;
Vпр — объем производства (за период);
Ркон — остатки нереализованной продукции на конец периода;
**[ МНК — Базовый метод регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных]
***[Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 (среднее значение случайной величины) и стандартным отклонением σ = 1 (рассеивание значений случайной величины относительно её математического ожидания, σ² — дисперсия (мера разброса)) . Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение стремится к нормальному.
**** Регрессионная модель – экономико-статистическая модель, основанная на уравнении регрессии, связывающем величины экзогенных (независимых, объясняющих) переменных x, влияющих на y ( на кол-во товаров оказывают влияние наличие ресурсов и уровень технологий) и эндогенной (зависимой, выходной) переменной y, являющейся объектом изучения (кол-во товаров):
у = f(x, b) + ε, где ε — линейная регрессия (случайная ошибка модели), если функция регрессии имеет вид f(x, b) = b0+b1x1+b2x2+…+bkxk
Эта функция может отражать зависимость спроса у на продукцию (услуги) от ее цены ее (в данном случае β < 0) или от дохода х (в данном случае β > 0. Функция может отражать также зависимость объема выпуска продукции у от использования ресурса х (производственная функция), в которой 0 < β < 1
***** Эласти́чность (англ. elasticity) — мера чувствительности одной переменной (например: спроса или предложения) к изменению другой (например: цены, дохода), показывающая на сколько процентов изменится первый показатель при изменении второго на 1%. Если коэффициент эластичности по модулю меньше единицы, то говорят о неэластичности переменной y по x. Если коэффициент эластичности больше 1, то говорят, что y эластичен по x, так как каждый процент изменения фактора приводит к ещё большему изменению y. Если коэффициент эластичности равен 1, то говорят о единичной эластичности. В предельном случае, когда коэффициент эластичности равен бесконечности, говорят о совершенной эластичности. Соответственно, при нулевом коэффициенте эластичности — о совершенной неэластичности.
****** Функция Кобба — Дугласа — зависимость объёма производства Q от создающих его факторов производства — затрат труда K и капитала L. Общий вид функции: Q=FKαLβ, где — технологический коэффициент, α — коэффициент эластичности по капиталу, β — коэффициент эластичности по труду.
ЗАКЛЮЧЕНИЕ
Логарифмы служат для существенного упрощения трудоёмких вычислений. В эконометрике логарифмирование применяется для преобразования экспоненциальных рядов в линейные, получения адекватных статистических выводов в результате отсутствия неоднородной дисперсии, для финансовых рядов их распределение в результате логарифмирования принимает нормальный вид, при логарифмировании регрессионной модели коэффициент при объясняющей переменной не что иное как эластичность. Логарифмирование производственной функции Кобба-Дугласа анализе производственных функций позволяет определить показатель отдачи от масштаба.
СПИСОК ЛИТЕРАТУРЫ
Интернет источники:
1. https://ru. wikipedia. org/wiki/Логарифм — Материал из Википедии — свободной энциклопедии
2. http://nsu. ru/ef/tsy/ecmr/Forum/topic11.htm — Конференция по эконометрике » Логарифмирование
3. http://www. irbis. vegu. ru/repos/11446/HTML/118.htm — Библиотека НОУ ВПО Академии ВЭГУ Логарифмические модели


