Частные коэффициенты корреляции

где Y — объем производства,

К — затраты капитала,

L — затраты труда,

a и b — коэффициенты частной эластичности Y по К и L: ЕК(Y)=a, ЕL(Y)=b.

С учетом влияния возмущений функция Кобба-Дугласа может выглядеть как мультипликативная степенная модель:

Эту модель можно свести к линейной относительно параметров путем логарифмирования обеих частей:

Если в формуле (4.5) принять, что при увеличении затрат К и L на расширение масштабов производства в несколько раз объем производства возрастает в такое же число раз, то a+b=1 и функция Кобба-Дугласа примет вид: Y = AKaL1-ae или:

где Y/L — производительность труда (руб./чел. за год),

K/L — капиталовооруженность (руб./чел. в среднем за год).

Для оценки параметров модели (4.7) ее нужно прологарифмировать.

Еще один вариант функции Кобба-Дугласа учитывает фактор экспоненциального роста технического прогресса:

где t — время, а q — темп прироста объема производства вследствие технического прогресса. Эта модель также приводится к линейному виду путем логарифмирования.

4.7. Частные коэффициенты корреляции

Часто возникает необходимость исследовать частную корреляцию между переменными при исключении — элиминировании — влияния остальных переменных. Выборочный частный коэффициент корреляции между переменными Хi и Xj при фиксированных остальных р-2 переменных определяется выражением:

где qii и qjj — алгебраические дополнения элементов rii и rjj матрицы коэффициентов корреляции (для частного случая р=3):

Пример 4.4.

Записать выражение (4.9) для случая трех переменных (р=3) относительно частного коэффициента корреляции r1-2,3 и вычислить его значение на основе корреляционной матрицы (4.10).

Решение.

Построим алгебраические дополнения на основе матрицы (4.10), а затем и само выражение (i=1, j=2, k=3):

Если взять значения коэффициентов корреляции r12=0,6; r13= r23=0,8, то получим отрицательное значение частного коэффициента корреляции: r1-2,.3=-0,11.

Смысл частного коэффициента можно получить из следующих рассуждений. Пусть имеется уравнение регрессии х1=bо+b1х2+b2х3+e. Требуется оценить корреляцию между Х1 и Х2 при исключении влияния Х3.

Для решения найдем два уравнения регрессии:

=bо+b1х3 и = +х3.

Коэффициент корреляции между остаткам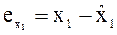и и отражает тесноту частной корреляции между переменными Х1 и Х2.

Таким образом, обычный коэффициент корреляции между остатками равен частному коэффициенту между самими переменными.

Как и обычный, частный коэффициент корреляции принимает значения от -1 до +1.

Значимость частного коэффициента корреляции ri-j,1,2,…,p оценивается так же, как и обычного коэффициента r, полагая объем выборки n’=n-p+2.

Вопросы для самоконтроля

1.  Какие алгебраические и содержательные неприятности влечет высокая мультиколлинеарность?

2.  Как выявляют и уменьшают степень мультиколлинеарности по матрице парных коэффициентов корреляции?

3.  В чем суть метода отбора значащих факторов и уменьшения мультиколлинеарности методом вращения факторов?

4.  Сколько нужно построить уравнений регрессий и вычислить оценок остаточной дисперсии s2 при отборе факторов методом вращения для исходного уравнения с четырьмя объясняющими переменными?

5.  Приведите произвольный исходный числовой пример для метода Чоу с двумя парами выборок.

6.  Нарисуйте бинарное дерево классификации регрессии.

7.  К какому классу нелинейности относится регрессия

у = bо+ b1 / x + e?

8.  Приведите степенную функцию: у = bо xb1e к линейному виду. К какому классу нелинейностей относится эта функция?

9.  Что означает “средний коэффициент эластичности”?

10.  У какой функции регрессии функция эластичности есть константа?

11.  Какой смысл и какие размерности имеют переменные и параметры функции Кобба-Дугласа? Получите сами значения частных коэффициентов эластичности этой функции.

12.  Что называется элиминированием переменных?

13.  В чем смысл частного коэффициента корреляции?

5. Регресионные модели временных рядов
и прогнозирование

5.1. Структура и классификация временных рядов

Временным (динамическим) рядом называется последовательность значений (уровней) переменной, измеренной в последовательные моменты времени: уt (t=1, 2,…, n), где n — длина ряда (число уровней).

В структуре экономических временных рядов в общем случае выделяют четыре составляющих (слагаемых):

уt = ut +nt +ct +et,

(5.1)

где	ut	— тренд, отражает основную долговременную тенденцию изменения признака – явления;
	nt	— сезонная составляющая, отражает цикличность изменения значений признака на внутренних относительно небольших (микро — и мезоуровнях) интервалах наблюдения (неделя, месяц, время года и т. п.;
	ct	— циклическая компонента, отражает цикличность изменения значений признака на внутренних больших интервалах наблюдения (макроуровнях) типа циклов солнечной активности Чижевского, волн Кондратьева, демографических ям и т. п.;
	et	— случайная составляющая, отражает влияние не поддающихся учету случайных факторов.

Первые три составляющие являются неслучайными, закономерными. Поэтому полной задачей анализа временного ряда является выявление всех этих трех закономерностей. Частной задачей может быть выявление какой-либо пары закономерностей из трех — это зависит от особенностей ряда и цели исследования.

Однако не всегда ряды содержат все три неслучайных составляющих, либо они пренебрежимо малы, либо их оценка невозможна ввиду ограниченности статистического материала, либо, наконец, это не диктуется целью исследования.

Классической задачей анализа временных рядов является выявление одной главной закономерности — тренда.

Наиболее распространенные методы исследования: корреляционный и спектральный анализы, модели авторегрессии и скользящей средней.

Важнейшей классификацией временных рядов (процессов) является их деление на стационарные и нестационарные. Временной ряд уt (t=1, 2,…, n) называется строго стационарным (или стационарным в узком смысле), если совместное распределение вероятностей n наблюдений у1+t, у2+t, … , уn+t не зависит от n, t и временного сдвига t. Поэтому характеристики распределения МО ay(t)=а, СКО sy(t)=s можно оценить на основе наблюдений уt (t=1, 2,…, n) по формулам:

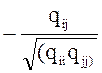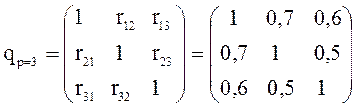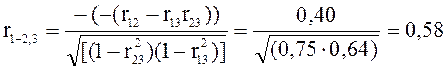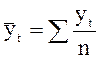, Наташа Автор Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку. Распродажа дипломных  Скидка 30% по промокоду Diplom2020 Подпишись на наш паблик в ВК  Получи промокод на скидку 20% Нужна работа? Дипломная работа у наших партнеров