Автокорреляционная функция
(5.2)
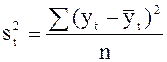 .
.
(5.3)
Классическим стационарным рядом в узком смысле является случайный процесс типа "белый шум", у которого МО ay(t)=0, а возмущения et некоррелированы между собой. Таким образом, возмущения et в классической линейной регрессионной модели образуют белый шум, а в случае их нормального распределения — нормальный белый шум.
Временной ряд уt (t=1, 2,…, n) называется стационарным (в широком смысле), если лишь числовые характеристики совместного распределения вероятностей n наблюдений у1+t, у2+t, … , уn+t не зависят от n, t и временного сдвига t. Содержательно стационарный ряд отражает процесс эволюции наблюдаемого явления.
При нарушении условия постоянства числовых характеристик временной ряд называется нестационарным. Нестационарный ряд отражает переход из одного устойчивого состояния в другое — развитие (деградация), у него есть начало и конец. Стационарный ряд может быть одной из составляющих нестационарного ряда.
5.2. Автокорреляционная функция
Важной характеристикой временных рядов является автокорреляционная функция r. Для стационарных рядов она зависит только от одной неслучайной переменной — временного сдвига (лага) t, для нестационарных — от двух переменных: сдвига (лага) t и момента начала отсчета t. Автокорреляционная функция определяется аналогично коэффициенту корреляции:
|
|
(5.4) |
Статистической оценкой r(t) является выборочная автокорреляционная функция r(t). График этих функций называют коррелограммой:
|
|
(5.5) |
Свойства автокорреляционной функции (рис. 5.1):
1. r(t)=r(-t) — функция четная.
2. r(t=0)=1.
3. При t®¥ çr ç®0.
|
r |
|
|||||
|
|
|
|||||
|
|
||||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|
|
|||
|
0 |
1 2 |
|
|
6 7 |
|
t |
|
|
Рис. 5.1. Типичная автокорреляционная функция временного ряда
с циклической составляющей
Значения r(t=1), r(t=2), … называются коэффициентами корреляции 1-го порядка, 2-го порядка и т. д. (рис.5.1).
Существует также частная автокорреляционная функция rчаст(t) и ее выборочный аналог rчаст(t). Например, выборочный частный коэффициент автокорреляции 2-го порядка между членами временного ряда yt и yt+2 при устранении влияния yt+1 вычисляется по формуле:
|
|
(5.6) |
где r(1), r(1,2), r(2) — выборочные коэффициенты автокорреляции между yt и yt+1, yt+1 и yt+2, yt и yt+2.
Автокорреляционная функция дает представление о характере временного ряда и помогает подобрать наиболее подходящую функцию регрессии.
5.3. Сглаживание временного ряда и прогнозирование
Одна из важнейших задач исследования временного ряда — выявление в нем основной тенденции, которая выражается неслучайной составляющей f(t). Последняя может быть трендом, либо трендом с циклической составляющей, либо трендом с циклической и сезонной составляющими — это зависит от цели исследования.
Выбор конкретной сглаживающей функции f(t) — сложная неформальная процедура. Для выбора используются по меньшей мере три типа информации.
Использование содержательной информации – семантический подход. Здесь строится качественная теория изучаемого процесса. Выдвигается гипотеза о причинах именно такого поведения процесса в прошлом и настоящем и о поведении в будущем. Например, при прогнозировании численности населения Калининградской области на период до 2020 г. мы имеем: устойчивый рост примерно до 1990 г., резкое сокращение примерно до 1998 г., постепенное уменьшение скорости сокращения до настоящего времени. Гипотеза: начавшийся подъем экономики, политическая стабилизация в течение нескольких лет остановят падение и начнется рост населения с постепенной стабилизацией на определенном уровне (по образцу западных стран).
Использование графической информации. Здесь временной ряд представляется в виде графика. Результаты наблюдения и содержательной теории о прошлом, настоящем и будущем процесса наносятся на этот график. Соответственно ему подбирается функция f(t) – линейная, или квадратичная, или степенная и т. п.
Использование аналитической информации. На основе содержательной и графической информации выбираются несколько функций, для каждой из которых строится регрессионное уравнение и рассчитываются показатели качества сглаживания (обычно с использованием компьютера), например, остаточная дисперсия, коэффициент детерминации, скорректированный коэффициент детерминации и др. На основе такой аналитической информации решается — обычно экспертным путем — задача многокритериального выбора наилучшей сглаживающей функции f(t).
При прочих равных условиях рекомендуется отдавать предпочтение более простым функциям, например, линейным. Заметим также, что задача сглаживания часто решается в комплексе с задачей прогнозирования.
Наиболее часто используются такие функции:
|
— линейная |
f(t)=bo+b1t |
|
— полиномиальная n-го порядка |
f(t)=bo+b1t+ … + bntn |
|
— логиcтическая Узнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
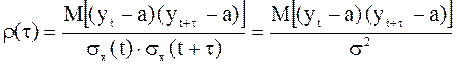 .
.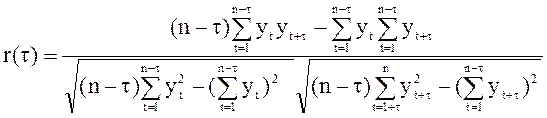 .
.


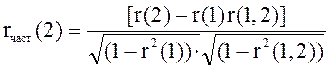 ,
,

