Сравнение влияния объясняющих переменных

Опустим все промежуточные преобразования (подробности см. [5, с. 84] ) и получим результат: систему нормальных уравнений в матричной форме относительно искомого вектора b:

Для наглядности представим данное матричное выражение графически (рис. 3.1). Полезно сравнить этот рисунок и выражение (3.6), определить размерности матриц. Напомним, что произведение матриц определяется как повторение одной и той же операции: скалярное произведение очередной строки левой матрицы на очередной столбец правой матрицы, что условно и показано на рис. 3.1.

X Y

X’ b X’
x x = x
Рис. 3.1. Графическое представление матричного выражения (3.6)

Чтобы разрешить систему (3.6) линейных уравнений относительно вектора b, нужно обе части уравнения умножить слева (умножение матриц некоммутативно) на матрицу, обратную к матрице Х’X, т. е. на (Х’X)-1. В результате получим систему линейных уравнений, разрешенную относительно вектора b:

Теперь можно предпосылку-6 переформулировать более конструктивно: матрица Х’X должна быть неособенной, иначе говоря, ее определитель не должен равняться нулю: êХ’X ê¹ 0. Еще одно эквивалентное условие: матрица Х’X должна иметь обратную матрицу.

Если воспользоваться стандартным пакетом программ, то именно в матричной форме удобнее всего формулировать задание (3.7) для компьютера.

Переформулируем предпосылки специально для матричной формы множественного регрессионного анализа:

1.  В модели (3.2) e — случайный вектор, Х — неслучайная матрица.

2.  М(e) = 0n, где 0n, — вектор-столбец, состоящий из n нулей.

3.  Одновременно и условие 4. åe = М(ee‘) = s2Еn, где Еn — единичная матрица n x n (заметим, что квадратная матрица получается в результате умножения по правилам матричной алгебры матрицы-столбца на матрицу-строку).

5. e — случайная величина-вектор с n-мерным НЗР Nn(0, s2Еn).

6. Ранг матрицы r(X) = p+1, причем p+1< n (неравенство требует, чтобы число наблюдений n было больше, чем число объясняющих переменных плюс 1).

Теорема Гаусса-Маркова. При выполнении предпосылок 1-4 и 6 множественного регрессионного анализа оценка по МНК b = (Х’X)-1X’Y является эффективной, т. е. обладает наименьшей дисперсией в классе линейных несмещенных оценок.

3.3. Сравнение влияния объясняющих переменных

При исследовании явления с помощью модели множественной регрессии часто бывает необходимым сравнить влияние объясняющих переменных на зависимую переменную. Иногда это можно сделать прямо по значениям коэффициентов регрессии bi. Однако чаще всего они имеют разную размерность и их влияние трудно сопоставить. Поэтому используют стандартизованные коэффициенты регрессии bj’ и коэффициенты (или функции) эластичности Ej (j=1, 2, … , p):

и

Стандартизованный коэффициент регрессии bj’ показывает, на сколько величин sy изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на sxj.

Средний коэффициент эластичности показывает, на сколько процентов изменится в среднем Y при увеличении одной переменной xj в окрестности значения на 1%.

Пример 3.1. На основе данных примера 2.1, табл. 2.2 для регрессии =76,88-0,35x рассчитать и раскрыть смысл стандартизованного коэффициента b1’ и коэффициента эластичности E1.

Решение. По формуле (3.8) b1’ = b1 sx1 / sy = -0,35×5,86 / 5,84 = -0,35 (в нашем случае значение практически не изменилось). Итак, при увеличении среднесуточного дохода х1 на sx1 =5,86 (руб.) доля расходов на питание уменьшится на 0,35 (%). Заметим, что в данном примере объясняемая переменная измеряется в процентах по условию.

Коэффициент эластичности: = bj/ = -0,35×54,9/57,89 = -0,33. Таким образом, при увеличении суточного дохода на 1% доля расхода на питание сокращается на 0,33%.

3.4. Выборочные оценки и доверительные интервалы

В многомерном регрессионном анализе матричным аналогом дисперсии одной переменной является ковариационная матрица åb вектора оценок параметров b:

,

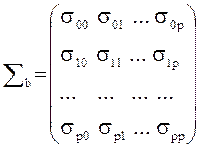где sij = M[(bi-M(bi))×(bj-M(bj))] — ковариации (корреляционные моменты) оценок параметров bi и bj. На главной диагонали этой матрицы находятся дисперсии оценок параметров регрессии:

sii = M[(bi-M(bi))×(bi-M(bi))] = sbi2.

Путем преобразований (см. [5, с. 92]) получаем ковариационную матрицу:

Таким образом, с помощью обратной матрицы (Х’X)-1 определяется как сам вектор оценок b, так и дисперсии-ковариации его компонент.

Выше мы показали, что оценка b вектора b по МНК является несмещенной и обладает наименьшей дисперсией, т. е. является эффективной (“наилучшей”).

Рассмотрим оценку дисперсии s2 возмущений e=Y – Xb (подробный вывод см. [5, с. 95]). Соответствующее выражение для несмещенной выборочной оценки s2 параметра s2 возмущений e:

Оценим значимость коэффициентов bj множественной регрессии, а затем и доверительного интервала для них.

Нулевая гипотеза Но: b= 0 отвергается с уровнем значимости a, если:

Поэтому доверительный интервал для параметра bj:

Аналогично доверительному интервалу (2.26) для Мх(Y) парной регрессии построим доверительный интервал для условного МО Мх(Y) множественной регрессии:

где — групповая средняя, определяемая по уравнению регрессии;

= — стандартная ошибка групповой средней ; Наташа Автор Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку. Распродажа дипломных  Скидка 30% по промокоду Diplom2020 Подпишись на наш паблик в ВК  Получи промокод на скидку 20% Нужна работа? 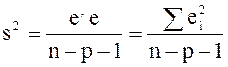Дипломные у наших партнеров