Основные распределения случайных величин
1.3. Основные распределения случайных величин
1. Дискретная СВ имеет биноминальный ЗР, если она принимает значения 0, 1, 2, … , m, … , n с вероятностями (формула Бернулли):
| Р(Х=m) = |
(1.12) |
где 0 < p < 1, q = 1-p, m = 0, 1, … ,n.
Биноминальный ЗР представляет собой закон распределения числа X = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одинаковой вероятностью р. Числовые характеристики ЗР: М(Х) = np, D(X) = npq.
2. Дискретная СВ Х имеет ЗР Пуассона, если она принимает значения 0, 1, 2, … ,…, m, … с вероятностями:
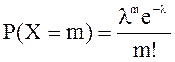 . . |
(1.13) |
Для ЗР Пуассона М(Х) = l, D(X) = l.
3. Непрерывная СВ Х распределена по показательному (экспоненциальному) ЗР, если ее плотность вероятностей имеет вид:
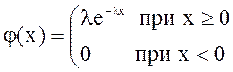 |
(1.14) |
Числовые характеристики: М(Х) = 1/l, D(X) = 1/l2.
4. Непрерывная СВ Х распределена по равномерному ЗР, если ее плотность вероятности имеет вид:
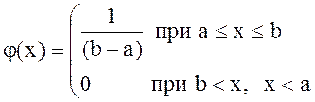 |
(1.15) |
Числовые характеристики ЗР: М(Х) = (a+b)/2, D(X) = (b-a)2/12.
5. Непрерывная СВ Х имеет нормальный ЗР (закон Гаусса), если ее плотность вероятности имеет вид:
jN(х) = 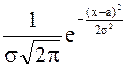 . . |
(1.16) |
Числовые характеристики ЗР: М(Х) = a, D(X) = s2 . Если а=0 и s2=1, то такой нормальный ЗР называется стандартным (нормированным). С его помощью определяется функция (интеграл вероятностей) Лапласа, которая равна площади под стандартной нормальной кривой N(0, 1) на отрезке [-х, х]:
Ф(х) = 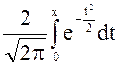 .
.
Через функцию Лапласа выражается нормальная функция распределения СВ Х :
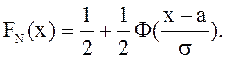 |
(1.17) |
Свойства СВ Х, распределенной по НЗР:
1) Вероятность попадания СВХ в интервал [-х, х]:
P(x1 £ X £ x2) = 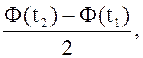 |
(1.18) |
где t1 = (x1- а)/s и t2 = (x2- а)/s.
2) Вероятность того, что отклонение СВ Х от МО а не превысит некоторую D>0, равна:
| P(| X-а| £ D) = Ф(t), | (1.19) |
где t=D/s.
Отсюда вытекает правило трех сигм: если СВ Х имеет ЗР N(a, s2), то практически достоверно, что ее значения заключены в интервале (а-3s, а+3s).
6. Распределением c2 (хи-квадрат) с k степенями свободы называется распределение суммы квадратов k независимых СВ, распределенных по стандартному НЗР:
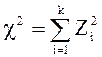 , , |
(1.20) |
где Z i имеет ЗР N(0, 1).
7. Распределением Стьюдента (t-распределением) называется распределение СВ t:
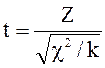 , , |
(1.21) |
где Z — СВ с НЗР N(0, 1), c2 — не зависимая от Z СВ с c2-распределением с k степенями свободы. Уже при k > 30 распределение можно считать нормальным.
8. Распределением Фишера-Снедекора (F-распределением) называется распределение СВ F:
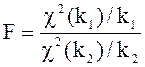 , , |
(1.22) |
где c2(k1) и c2(k2) — СВ, имеющие c2 — распределения с k1 и k2 степенями свободы.
1.4. Многомерные случайные величины и условные законы распределения
Упорядоченный набор Х= (X1, X2, … , Xn ) случайных величин называется n-мерной СВ.
Функцией распределения n-мерной СВ (X1, X2, … , Xn ) называется функция F(x1, x2, … , xn), являющаяся вероятностью совместного выполнения n неравенств:
| F(x1, x2, … , xn) = Р(Х1< х1, Х2< х2, … , Хn< xn). | (1.23) |
Двумерная функция распределения:
| F(x, y) = Р(Х< х, Y< y). | (1.24) |
Свойства ФР F(x, y):
1. 0 £ F(x, y) £ 1.
2. Если x1 < x2, то F(x1, y) £ F(x2, y), аналогично и для y1 < y2 .
3. F(x, -¥) = F(-¥, y) = F(-¥,-¥) = 0.
4. F(x, ¥) = F1(x), F(¥, y) = F2(y), где F1(x) и F2(y) — функции распределения СВ Х и Y соответственно.
5. F(¥,¥) = 1.
Плотностью вероятности (совместной плотностью) непрерывной двумерной СВ (Х, Y) называется вторая смешанная частная производная ее ФР:
j(x, y) = Fxy”(x, y) = 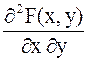 |
(1.25) |
Свойства плотности вероятности двумерной СВ j(x, y):
1. j(x, y) ³ 0.
2. P((x, y) Î D) = 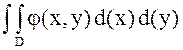 .
.
3. F(x, y) = 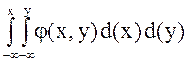 .
.
4. 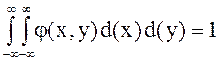 .
.
Условным ЗР СВ Х, взятой из двумерной СВ(Х, Y), называется закон распределения СВ Х, полученный при условии, что другая СВ Y приняла определенное значение. Условная плотность вероятности jy(x) двумерной СВ (Х, Y) определяется формулой:
jy(x) = 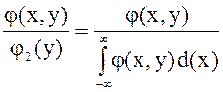 .
.
Числовые характеристики условного распределения: условное МО а(у)=Му(Х) и условная дисперсия s2(у)=Dy(X). Другие их обозначения: М(Хêу) и D(Хêу).
Условное МО СВ Y при Х=х, т. е. Мх(Y), есть функция от х, называемая функцией регрессии (регрессией) Y по Х.
Пример. Пусть двумерная СВ (Х, Y) и ее ЗР j(x, y) являются некоторой моделью железной дороги, причем СВ Х — количество порожних вагонов в суточной заявке порта, СВ Y — количество поставленных порожних вагонов за сутки в порт. Тогда регрессия Мх(Y) показывает соотношение между заявкой и поставкой вагонов в среднем (рис. 1.3).
 |
| Мх(Y) (шт.) | |||||||


