Критерий чоу: объединение регрессий

Таблица 4.1

Включение булевских переменных в регрессию

На основе этой таблицы легко выписать смысл значения булевских переменных: z1=1, если высшее и z1=0 иначе; z2=1, если среднее профессиональное и z2=0 иначе; если z1=0 и z2=0, то среднее (другого не дано).

4.3. Критерий Чоу: объединение регрессий

Пусть Y — среднемесячная зарплата (руб.), Х — продолжительность образования (лет). Пусть у нас имеются две пары выборок Y и Х объемами n1 и n2: одна пара — для мужчин, другая — для женщин. Вопрос: можно ли объединить эти пары, проигнорировав различие полов, и построить одну надежную модель по большой выборке объемом n1+ n2 ?

По методу Чоу строятся две линейные регрессионные модели с коэффициентами-векторами b‘ и b,,. Нулевая гипотеза Но: b‘ = b,, и D(e‘)=D(e,,)=s2, где e‘ и e,,- вектора-возмущения двух регрессий. Если Но верна, то эти две регрессионные модели схожи и объединяются в одну, т. е. строится единая модель по паре выборок объемом n1+n2 .

Нулевая гипотеза Но отвергается с уровнем значимости a, если выполняется неравенство — критерий Чоу:

где å — оператор суммирования по i от 1 до n (по ошибкам объединенной регрессии), å’ — оператор суммирования по i от 1 до n1, å» — оператор суммирования по i от n1+1 до n.

4.4. Нелинейные регрессионные модели: классификация

и примеры

Вопрос нелинейности регрессионной модели не решается однозначно. Существует довольно сложная классификация нелинейных моделей (подробно см. работу [6, с. 124] и табл. 4.2).

Таблица 4.2

Классификация уравнений регрессии

Опишем классы нелинейных регрессий и приведем примеры моделей.

Класс Н1: нелинейные относительно включенных в них переменных, но линейные по оцениваемым параметрам.

Примеры:

—  полином второй степени: у = bо+b1x + b2x2 + e;

—  полином третьей степени: у = bо+ b1x + b2x2 + b3x3 + e;

—  равносторонняя гипербола: у = bо+ b1 / x + e.

—  полулогарифмическая функция: у = bо+ b1 lnx+ e;

Модели этого класса определяются как и линейные, с помощью МНК путем замены переменных. Например, в параболе второй степени заменим переменные: x = х1, x2= х2 и получим двухфакторное уравнение линейной регрессии:

у = bо+ b1x1 + b2x2 + e.

Класс Н2: нелинейные по параметрам:

—  степенная: у = bо xb1 e,

—  показательная: у = bо b1xe,

—  экспоненциальная: у = еbо + b1хe.

Этот класс делится на два подкласса, которые мы и рассмотрим ниже.

Класс Н.2.1: нелинейные по параметрам модели, но внутренне линейные.

Примеры:

—  степенная: у = bо xb1e,

—  экспоненциальная: у = еb0 + b1х e.

Модели этого класса после преобразования к линейному виду также решаются МНК. Например, прологарифмировав степенную фукцию, получим: lny = lnbо + b1 lnx+ lne. Заменим переменные: lny = z, lnbо =bо’; lnx = u, lne = e‘. Получаем линейное уравнение регрессии:

z = bо’+ b1u +e‘.

Класс Н.2.2: нелинейные модели — внутренне нелинейные.

Примеры:

—  степенная: у = bо xb1 + e (отличие от рассмотренной выше функции в том, что возмущение здесь не мультипликативно, а аддитивно);

—  гиперболическая: .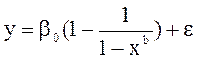

Для подобных моделей МНК может быть применен только в форме специальных поисковых процедур, т. к. аналитически соответствующая система уравнений не разрешается. Примеры таких процедур вычислительной математики: метод наискорейшего спуска Коши, модифицированный метод Ньютона, метод покоординатного спуска и пр.

4.5. Функции эластичности

Функции эластичности представляют большой экономический интерес при анализе явления на основе эконометрической модели. Для начала выведем несколько функций эластичности, а потом просто приведем их в табл. 4.3. Напомним, что функция эластичности означает: на сколько процентов изменился при изменении переменной хi ровно на 1%.

Таблица 4.3

Примеры функций эластичности

По определению частной функцией эластичности Еxi() множественной регрессии =f(x1, x2, … , xр) является функция

.

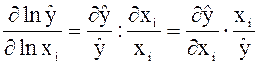Итак, функция эластичности имеет вид:

Пример 4.2.

Дано линейное уравнение регрессии =5+6×1-2×2, выборочные средние: =10, =20, =25. Найти частную функцию эластичности по переменной х2.

Решение.

По формуле (4.3) искомая функция: Еx2() = ¶/¶x2 ×x2/ = -2×2/(5+6×1-8×2). Можно положить =10, и получим частную функцию эластичности Е(x2)= -2×2/(65-8×2). Наконец, для =20 можно получить средний частный коэффициент эластичности по x2: =-0,89%. Итак, в окрестности выборочных средних увеличение x2 на 1% приводит к уменьшению на 0,89%.

Пример 4.3.

Дано парное уравнение регрессии со степенной функцией: =5×х1/2. Найти функцию и средний коэффициент эластичности.

Решение.

Еx()==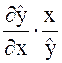= 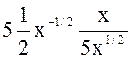0,5.

Итак, функция эластичности для степенной функции есть константа.

4.6. Производственная функция Кобба-Дугласа

В качестве примера линеаризующего преобразования рассмотрим одну из многих типов производственных функций — функцию Кобба-Дугласа:
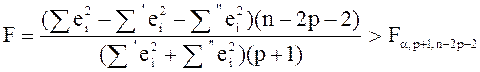